alice
manual.

This page is meant as a short introduction to the Alice language and system and its features:
Alice ML is an extension of the Standard ML language (SML). Most of the examples shown here assume a working knowledge of functional programming in general and SML in particular. There are numerous books and tutorials available for SML.
Online Material:
Paper Books:
The definition of the language and its library can be found here:
For a more comprehensive literature list, see the bibliography on the SML/NJ site.
Alice ML is an extension of Standard ML, and the Alice interactive toplevel works very similar to the interactive prompts known from other SML systems, where you can type in expressions and declarations to evaluate them. Input is terminated with a semicolon. For example, you might simply perform a simple calculation:
- 4+5; val it : int = 9
The expression is evaluated and the result 9 printed along with its inferred type int. Anonymous expressions get the name it, so that you can refer to them in consecutive inputs:
- 2*it; val it : int = 18
Note: We only use and describe the simple text interface to the toplevel in this tour. There also is a graphical frontend, which works similarly, but offers more features.
We can also try the one-line Hello World program:
- print "Hello world!\n"; Hello world! val it : unit = ()
Note: In the rest of this tour we will present program fragments in their pure form, without showing the interactive prompt or the semicolon terminating the interactive input. For example, the last interaction will be displayed simply as
print "Hello world!\n" Hello world! val it : unit = ()
Entering a function declaration is more interesting. For example, the factorial function:
fun fac 0 = 1 | fac n = n * fac (n-1) val fac : int -> int = _fn
This time, the result has a more complex type: it is a function from integers to integers. We can apply that function:
fac 12 val it : int = 479001600
If a computation takes too long you can abort it in the interactive toplevel by entering Ctrl-C. For example:
fun loop () = loop () val loop : unit -> '1 = _fn loop () <Ctrl-C> interrupted
Note: In the graphical interface to the toplevel you have to interrupt a computation by invoking the respective command from the Eval menu. The keyboard shortcut is Ctrl-I.
Unlike with other ML systems, you can also put a computation into background instead of interrupting it, by pressing Ctrl-Z (Ctrl-Break on Windows):
loop () <Ctrl-Z> val it : '1 = _future
This feature is useful if you still want to use the result of the computation later on but do not want to wait for it now. The result of a background computation is represented by futures, see the discussion of concurrency below.
The interactive toplevel (in text mode) is exited with Ctrl-D (Ctrl-Z on Windows), or by calling exit().
Note: Under Windows, depending on the shell used, Ctrl characters may not work as expected. We recommend using zsh under Cygwin, or the SML mode for Emacs. On Linux, certain command line editing tools like rlwrap might interfer with some of the Ctrl characters as well. In case of problems, we suggest using the graphical mode of the toplevel.
For more complex values, plain static output of the result is often insufficient. The Alice system includes the Inspector for browsing arbitrary data structures interactively:
inspect (List.tabulate (10, fn i => (i, i*i, i*i*i))) val it : unit = ()
An Inspector window will pop up displaying the table of square and cubic numbers:
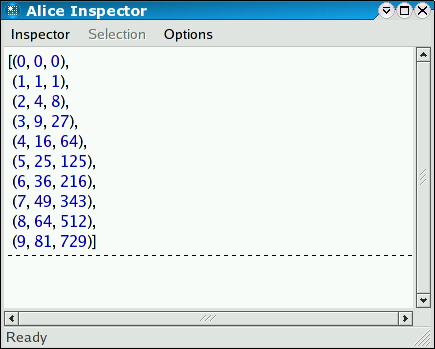
When you inspect additional values, they will be displayed in the same Inspector window. The inspector can be used to browse arbitrary data structures:
val r = ref 56
val r : int ref = ref 56
inspect (3 + 8, SOME 3.141592, {hello = "hello, world"}, r, [true, 4 < 3])
val it : unit = ()
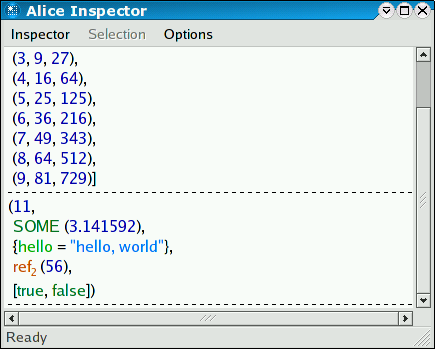
Note: If the size of the inspected data structure exceeds certain configurable limits, parts of the output will be hidden. Those parts are represented by dots, which can be interactively unfolded if desired.
Note the index put after the ref constructor in the Inspector window. All displayed references and futures are decorated by such an index to indicate which of them are identical.
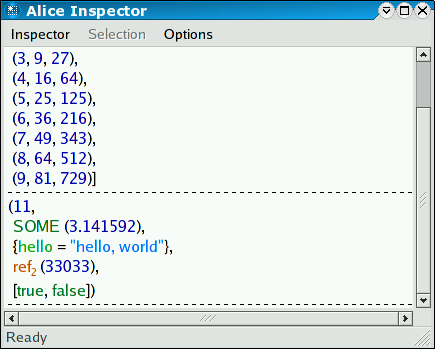
The Inspector concurrently watches the data structures it shows. If they change, it will automatically update its display. For example, if you re-assign a reference the Inspector window will be updated automatically:
r := 33033 val it : unit = ()
You can select any part of a displayed value by clicking on it. If you hover over the selection with the mouse the inspector will show the value's type as a tool tip.
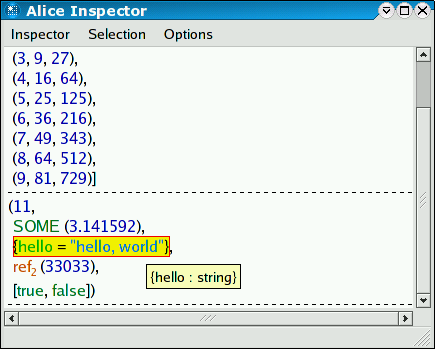
You can clear the Inspector window by choosing Clear from the Inspector menu.
While Standard ML is a fully eager (strict) language, Alice ML provides support for optional lazy evaluation. Any expression can be evaluated lazily by preceeding it with the lazy keyword:
val x = lazy 4+5 val x : int = _lazy
Lazy suspensions are represented by the _lazy notation in the interactive toplevel's output, as shown above. The value of x will not be computed before it is actually required. For example,
(x,x) val it : int * int = (_lazy, _lazy) x val it : int = _lazy fun pair x = (x,x) val pair : 'a -> 'a * 'a = _fn pair x val it : int * int = (_lazy, _lazy) x > 10 val it : bool = false x val it : int = 9
Tupling is parametric in its components and does not trigger x. Neither does applying it to a function whose body does not trigger its argument, like pair above. The comparison operator > is future-strict in its arguments, however, and hence forces evaluation of x. Likewise, pattern matching, arithmetic operations, comparison (op=) or similar operations can force a value.
As a simple example of a lazy function, consider a generator for lazy streams of numbers:
fun enum n = lazy n :: enum (n+1) val enum : int -> int list = _fn val ns = enum 0 val ns : int list = _lazy List.nth (ns,5) val it : int = 5 ns val it : int list = 0 :: 1 :: 2 :: 3 :: 4 :: 5 :: _lazy
In this example, requesting the 5th element of the list forced partial evaluation of the list, up to that element.
We can define a lazy variant of the map function:
fun mapz f xs = lazy (case xs of nil => nil
| x::xs' => f x :: mapz f xs')
val mapz : ('a -> 'b) -> 'a list -> 'b list = _fn
Note that the case expression must be nested inside the lazy expression - otherwise applying mapz would trigger evaluation of the head of the list, to perform the necessary pattern matching. Function declarations support syntactic sugar that allows expressing the same definition more elegantly:
fun lazy mapz f nil = nil
| mapz f (x::xs) = f x :: mapz f xs
val mapz : ('a -> 'b) -> 'a list -> 'b list = _fn
This derived form is defined such that both definitions of mapz are equivalent. Let us apply mapz to the stream of natural numbers to calculate their factorials lazily:
val facs = mapz fac (enum 0) val facs : int list = _lazy List.take (facs,7) val it : int list = [1, 1, 2, 6, 24, 120, 720] facs val it : int list = 1 :: 1 :: 2 :: 6 :: 24 :: 120 :: 720 :: _lazy
The Inspector observes when lazy suspensions are triggered. If you evaluate
inspect facs val it : unit = () List.nth (facs,10) val it : int = 3628800
it will automatically update its window to reflect the substitution of the lazy tail of facs by a (partial) list.

Here is a lazy version of the zip function:
fun lazy zipz (x::xs, y::ys) = (x,y) :: zipz (xs,ys)
| zipz _ = nil
val zipz : 'a list * 'b list -> ('a * 'b) list = _fn
It is possible to calculate the stream of Fibonacci numbers using mapz and zipz:
val rec fibs = 1 :: 1 :: (lazy mapz op+ (zipz (fibs, tl fibs))) val it : int list = 1 :: 1 :: _lazy List.nth (fibs, 10) val it : int = 89 fibs val it : int list = 1 :: 1 :: 2 :: 3 :: 5 :: 8 :: 13 :: 21 :: 34 :: 55 :: 89 :: _lazy
For more practical applications of laziness, see the standard literature on lazy functional programming. Last but not least, note that Alice ML allows laziness to be combined freely with side effects:
val n = lazy (print "Huhu!\n"; 13) val n : int = _lazy n+1 Huhu! val it : int = 14
Take care with side effects when you do lazy programming!
Alice extends SML with support for concurrency. Concurrency is light-weight: the system can handle tens or hundreds of thousands of concurrent threads. Concurrent programming in Alice is uniformingly based on the model of futures.
A concurrent thread can be initiated by means of the spawn expression:
spawn 45*68 val it : int = _future
In this example the value 45*68 is computed in a new thread. The result of the spawn expression is a future, a place-holder for the result of the concurrent computation. Once the result becomes available, the future will be globally replaced by the result. We say that threads are functional, in the sense that they have a result.
Note: If you do not happen to have an ancient machine then you most likely will not have seen the output above. Instead you have already seen the actual result of the computation, because it performed faster than the interactive toplevel was able to print it.
The semantics of futures becomes more obvious if we look at a thread that does not terminate immediately. For that purpose, let us define the naive version of the Fibonacci function, which has exponential complexity:
fun fib (0 | 1) = 1 | fib n = fib (n-1) + fib (n-2) val fib : int -> int = _fn
On an ordinary desktop PC, computing fib 35 will take quite some time. We perform that computation concurrently:
val n = spawn fib 35 val n : int = _future
We get back a future, that we can look at using the Inspector:
inspect n val it : unit = ()
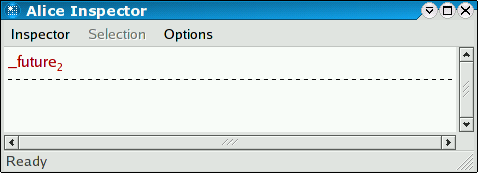
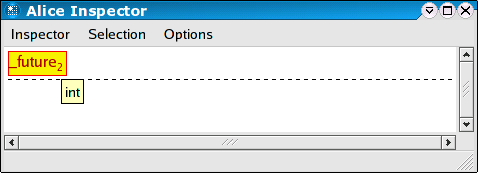
At first, the Inspector will display the value as a future, as shown above. You can investigate the type of the value the future is holding place for by using the tool tip feature:
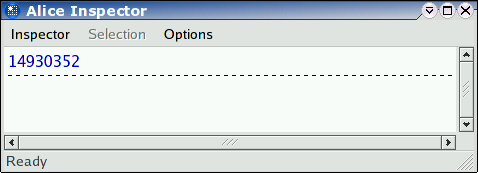
Once the computation of the result finishes and the thread terminates, the future gets replaced by the thread's result. The Inspector will update its display accordingly:
The situation becomes more interesting if we start several threads at once:
inspect (List.tabulate (10, fn i => spawn fib (i+25))) val it : unit = ()
The individual entries from the small table we build are calculated concurrently and become available individually. At some point in time the Inspector window might display the following:
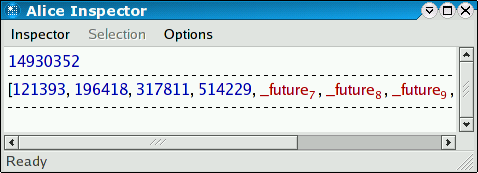
Futures can be passed around as values. Once an operation actually requests the value the future stands for, the corresponding thread will block until the future has been determined. This is known as data-flow synchronisation and is a powerful mechanism for high-level concurrent programming. As a trivial example, consider the following pair of concurrent producer and consumer that are connected through a message stream:
val delay = Time.fromSeconds (Int.toLarge 2)
val delay : Time.time = time{|2000000us|}
fun produce 0 = []
| produce n = spawn (Thread.sleep delay; n :: produce (n-1))
val produce : int -> int list = _fn
fun consume (n::ns) = (print (Int.toString n ^ "\n"); consume ns)
| consume nil = ()
val consume : int list -> 'a = _fn
spawn consume (produce 5)
val it : unit = _future
5
4
3
2
1
Synchronisation on futures can also be done explicitly, by employing the library function await:
await (spawn fib 30) val it : int = 1346269
Interestingly, lazy suspensions are nothing but a special form of future, called a lazy future. Requesting a lazy future is triggering the corresponding computation. Consequently, await can also be used to trigger lazy computations explicitly:
lazy 3+4 val it : int = _lazy await it val it : int = 7
What happens if a concurrent computation fails, e.g. by raising an exception? In that case the future will be failed. A failed future carries an exception indicating the cause of the failure. A failed future does not cause failure of a client by itself. Only when a client actually requests the failed future, the failure exception will be re-raised at the point of request:
spawn (raise Domain)
val it : 'a = _future
[1, it, 3]
val it : int list = [1, _failed{|Domain|}, 3]
10 * List.nth (it, 1)
uncaught exception Domain
In the second output, the interactive toplevel uses the notation _failed{|exn|} to indicate a future failed with exception exn.
See the manual page on futures for a detailed discussion of concurrency, futures, and failure.
Dealing with state correctly in a concurrent environment requires the availability of atomic operations. Alice provides an atomic exchange operation for references:
val r = ref 10 val r : int ref = ref 10 Ref.exchange (r, 20) val it : int = 10
The value of the reference is extracted and replaced in one atomic operation. See below for an example relying on this function.
Functional threads and lazy evaluation offer convenient means to create futures "on the fly". Often the direct coupling between a future and the computation delivering its result is too inflexible, however. For such cases, Alice offers promises.
A promise is an explicit handle for a future. When a promise is created,
open Promise
val fail : 'a promise * exn -> unit = _fn
val future : 'a promise -> 'a = _fn
val fulfill : 'a promise * 'a -> unit = _fn
val promise : unit -> 'a promise = _fn
val Promise : exn = Promise
exception Promise
type t = t
type promise = promise
val p : int promise = promise ()
val p : int Promise.promise = promise{|_future|}
an associated future is created along with it. This future can be obtained as follows:
val x = future p val x : int = _future
Such a promised future behaves like a concurrent future, in particular by allowing dataflow synchronisation. But unlike a concurrent or lazy future it does not vanish automatically, but has to be eliminated explicitly through the corresponding promise:
fulfill (p, 19)
val it : unit = ()
p
val it : int Promise.promise = promise{|19|}
x
val it : int = 19
Intuitively, by creating a future this way, you create a place-holder for a value that you "promise" to deliver at some later point in time. At that point, you "fulfill" your promise. A promise may only be fulfilled once. Hence, a different view on promises is that of a single assignment reference, yielding the following correspondences:
type 'a promise type 'a ref promise : unit -> 'a promise ref : 'a -> 'a ref future : 'a promise -> 'a ! : 'a ref -> 'a fulfill : 'a promise * 'a -> unit := : 'a ref * 'a -> unit
The important point is that a promise is not initialized (hence the difference in the constructor types), and dereferencing it prior to assignment delivers a place holder for its potential content.
Usage of promises is not necessarily related to concurrent programming. One application is the top-down construction of data structures, as opposed to the bottom-up construction usually required in functional programming. As a simple example of that we show how promises can be utilised to program a tail-recursive version of the list append function:
fun append (l1,l2) =
let
fun iter (nil, p) = fulfill (p, l2)
| iter (x::xs, p) =
let
val p' = promise ()
in
fulfill (p, x::future p'); iter (xs, p')
end
val p = promise ()
in
iter (l1, p); future p
end
val append : 'a list * 'a list -> 'a list = _fn
This formulation is somehwat reminiscent of the definition of append in logic programming. Its basic idea is to cons the head of the left operand to a future in each iteration. That future gets replaced by the actual tail in the next iteration, with the tail again containing a future as its respective tail. When we reach the end of the list, the last future gets replaced by the right operand.
In a similar vein, arbitrary data structures can be generated in a top-down manner by creating promised futures as place holders for parts of it and construct them afterwards.
The primary purpose of promises is to provide a simple primitive that enables the implementation of high-level concurrency abstractions. We only give an idea of that here, by showing how promises can encode another well-known concurrency idiom easily: channels.
A channel (sometimes also called a port) is a simple imperative message queue that allows asynchronous communication between processes. As an abstract data type it can be described by the following signature:
signature CHAN =
sig
type 'a chan
val chan : unit -> 'a chan
val put : 'a chan * 'a -> unit
val get : 'a chan -> 'a
end
An arbitrary number of messages may be sent to a channel using put. The get operation takes the oldest message out of the channel. It suspends if none is available. A more advanced design might distinguish between read and write view of a channel, but we ignore that here for the sake of simplicity.
A straight-forward implementation uses promises and references:
structure Chan : CHAN =
struct
open Promise
type 'a chan = 'a list promise ref * 'a list ref
fun chan () =
let
val p = promise ()
in
(ref p, ref (future p))
end
fun put ((putr,getr), x) =
let
val p' = promise ()
val p = Ref.exchange (putr, p')
in
fulfill (p, x::future p')
end
fun get (putr, getr) =
let
val p' = promise ()
val xs = Ref.exchange (getr, future p')
in
fulfill (p', tl xs); hd xs
end
end
The implementation is a variation of a difference list: the first reference stores the tail of the queue ("write position"), while the second points to the head ("read position"). Modification of either position is performed by an atomic exchange operation on the respective reference. That ensures that all operations are properly sequentialized.
The tail is represented as a promised future. As in the append example from the previous section this allows constructing the message queue incrementally in the put function.
By using a promised future in the implementation of get we can use atomic exchange although the new value actually depends on the previous one. Any concurrent get operation will block automatically (in tl) until the future is eliminated by fulfilling the promise. Consequently, no get operation can proceed before the former has determined the new queue. That ensures thread-safety.
Likewise, when the queue is empty, get encounters a future for xs and will block. This time, the future is eliminated by the next put operation.
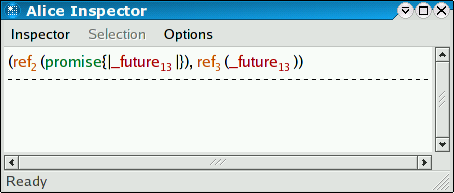
Let us create a channel and observe its content using the Inspector:
val ch : int Chan.chan = Chan.chan ()
val ch : int Chan.chan = (ref (promise{|_future|}), ref (_future))
inspect ch
val it : unit = ()
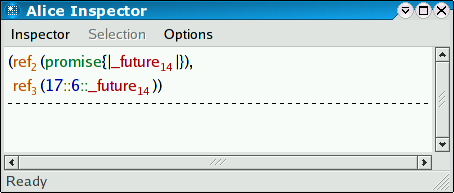
Chan.put (ch, 17); Chan.put (ch, 6) val it : unit = ()
(Chan.get ch, Chan.get ch) val it : int * int = (17, 6)
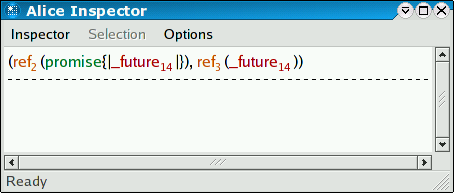
Tuples are always evaluated from left to right, so we will deterministically get the pair (17,6) in the last example. To witness non-determinism due to concurrency, let us set up several clients. They perform an expensive calculation before reading from the channel, in order to properly randomize thread scheduling:
fun client _ = spawn (fib 20; Chan.get ch) val client : 'a -> int = _fn inspect (List.tabulate (5, client)) val it : unit = () Chan.put (ch, 1); Chan.put (ch, 2); Chan.put (ch, 3) val it : unit = ()
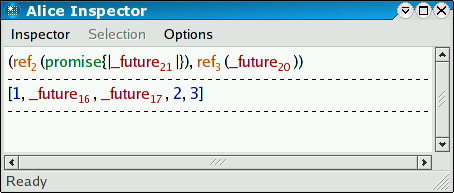
The order in which the threads will read from the channel is non-deterministic, but no value will ever get lost or read twice.
There is a tiny interactive demo demonstrating dataflow synchronisation using streams:
Compile with:
alicec streams.aml
Run with:
alicerun streams
One of the major pros of ML is its powerful static type system. However, there are programming tasks where it is not possible to perform all typing statically. For example, consider exchange of data structures between separate processes. To accompony such tasks of open programming, Alice complements its static type system with a controlled form of dynamic typing.
Alice provides the type package of dynamically typed values. A package essentially is a pair of a (higher-order) module and its signature. Packages are created using the pack expression:
val p = pack Word8 : WORD
val p : package = package{|...|}
This example injects the module Word8 into a package. The signature constraint (the part following the colon) is part of the pack expression. It specifies the package's signature. The packaged module must of course match that signature statically.
Using the Inspector, we can look inside the package:
inspect p val it : unit = ()
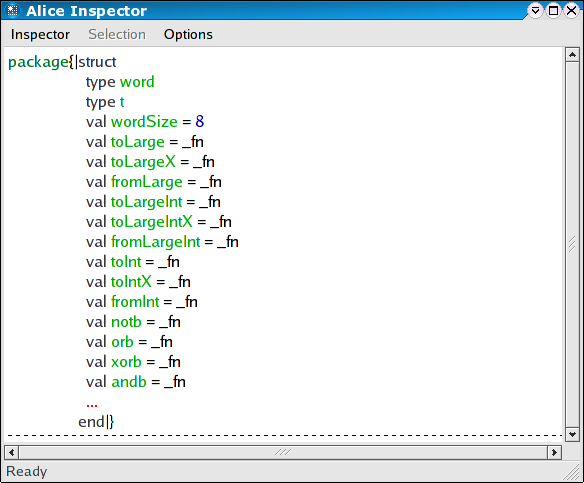
We can even investigate its signature:
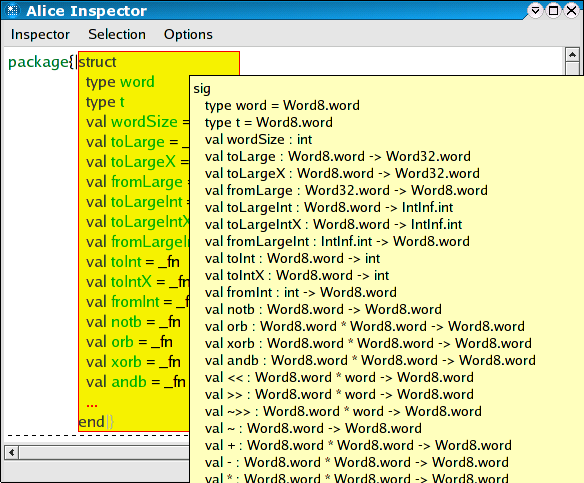
The package p may be passed to some client, which may unpack it as follows:
structure Word' = unpack p : WORD structure Word' : WORD
The unpack expression also requires a signature being specified. Unpacking involves a dynamic type check: to evaluate the expression, the package signature is matched against the specified target signature. If matching succeeds, the packaged module is returned. Otherwise, an exception is raised:
structure List' = unpack p : LIST uncaught exception Mismatch
If unpacking succeeds, the client may use the Word' structure as usual. The static signature of Word' is determined by the target signature specified with unpack.
Since modules can contain arbitrary values, any value can be wrapped up as packages. In particular, values can be given polymorphic type in packages:
val p = pack (val x = length) : (val x : 'a list -> int)
val p : package = package{|...|}
Note: This example uses some syntactic sugar of Alice ML, which allows replacing struct...end and sig...end by (...).
Unpacking may specify a more restrictive target signature:
structure IntLength = unpack p : (val x : int list -> int) structure IntLength : sig val x : int list -> int end structure RealLength = unpack p : (val x : real list -> int) structure RealLength : sig val x : real list -> int end
The whole range of SML signature matching rules applies, so a package may have more components than required by the target signature, may have more general value types, or more specific type components, etc. Using packages hence is quite robust with respect to extensions.
See the respective manual page for a more detailed look at the semantics of packages. Packages are the basis of several other features of Alice, in particular pickling and distribution.
Applications rarely run in isolation. Many applications need to exchange data with other applications, or make data persistent between runs. Consequently, it should be possible to export and import data from processes. Export of language data structures is often known as serialization, or pickling.
Alice provides high-level support for pickling, that is, arbitrary data can be pickled, including code and entire modules. Pickles are platform-independent and are hence suitable for exchange across heterogenous networks, especially the Internet. By pickling first-class functions, Alice processes can exchange behaviour.
The pickling library is based on packages. Consequently, the entities of import/export are modules. This implies that even types and signatures can be exchanged between processes. Consider a very simple abstract type as an example:
signature NUM =
sig
type t
fun fromInt : int -> t
fun toInt : t -> int
fun add : t * t -> t
end
signature NUM =
sig
type t
val fromInt : int -> t
val toInt : t -> int
val add : t * t -> t
end
structure Num :> NUM =
struct
type t = int
fun toInt n = n
fun fromInt n = n
val add = op+
end
structure Num : NUM
Note: For values of abstract type the toplevel prints place-holders only. However, the function Print.register can be used to install a user-defined printer for abstract types, e.g.
Print.register (Int.toString o Num.toInt)enables the toplevel to print values of type Num.t in integer representation. Likewise, printers can be installed for the Inspector, using the function Inspector.register.
A package can be formed from this structure and be written to a file:
Pickle.save ("Num.alc", pack Num : NUM)
val it : unit = ()
To recover the structure in another (or the same) process, one simply executes the inverse operation:
structure Num' = unpack Pickle.load "Num.alc" : NUM structure Num' : NUM Num'.toInt (Num'.add (Num'.fromInt 4, Num'.fromInt 5)) val it : int = 9
Note that the type Num'.t is incompatible with the original type Num.t:
Num'.add (Num.fromInt 4, Num.fromInt 5) 0.0-0.39: argument type mismatch: Num.t * Num.t does not match argument type Num'.t * Num'.t because type Num.t does not unify with Num'.t
The reason is that the signature annotation for unpack does not specify the necessary type equivalence - the types are statically incompatible, although we know they are the same dynamically. The usual means of expressing type sharing can be used to induce that knowledge statically:
structure Num' = unpack Pickle.load "Num.alc" : NUM where type t = Num.t
structure Num' :
sig
type t = Num.t
val fromInt : int -> Num.t
val toInt : Num.t -> int
val add : Num.t * Num.t -> Num.t
end
The result signature already indicates the type sharing, making legal
Num'.add (Num.fromInt 4, Num.fromInt 5) val it : Num'.t = _val
Note however, that the type Num'.t is still abstract and incompatible to int:
Num'.add (4, 5) v1.0-1.15: argument type mismatch: int * int does not match argument type Num'.t * Num'.t because type int does not unify with Num'.t
See the manual page on pickling for more detail on the semantics of pickling.
Alice introduces the notion of component as the unit of compilation as well as deployment. Superficially, a component contains a module expression that, when evaluated, potentially imports modules from other components. An application will consist of a set of components with one designated "main" or "root" component.
Consider the following trivial component:
(* Fac.aml *)
structure Fac =
struct
val _ = print "Evaluating component Fac...\n"
fun fac 0 = Int.toLarge 1
| fac n = Int.toLarge n * fac (n-1)
end
We can compile it invoking the Alice batch compiler from a shell:
alicec Fac.aml
If the interactive toplevel has been started in the same directory, the compiled component can be imported interactively:
import "Fac" ### loaded signature from file:/home/user/Fac structure Fac : sig val fac : int -> IntInf.int end = Fac
Loading is performed lazily: the interactive toplevel will load the signature from the component file, but it will not yet evaluate (execute) the component. This is appearent from the fact that the message contained in the structure has not been printed in the above example. We can also see it when accessing a structure field:
Fac.fac val it : int -> IntInf.int = _lazy
The function is represented by a lazy future. The component will be evaluated when its content is first requested:
Fac.fac 23 Evaluating component Fac... val it : IntInf.int = 25852016738884976640000 Fac.fac 46 val it : IntInf.int = 5502622159812088949850305428800254892961651752960000000000
Let us write a little application using the Fac component. We simply implement an appropriate main component:
(* Main.aml *)
import structure Fac from "Fac"
structure Main =
struct
fun main () =
let
val _ = TextIO.print "Input number: "
val n = valOf (Int.fromString (valOf (TextIO.inputLine TextIO.stdIn)))
in
TextIO.print (IntInf.toString (Fac.fac n) ^ "\n");
OS.Process.success
end
handle Option => (TextIO.print "error\n"; OS.Process.failure)
val _ = OS.Process.exit (main ())
end
This component imports the structure from the previous component by using an import announcement. Every component can be headed by an arbitrary number of such import announcements. The Main component is compiled in the usual way:
alicec Main.aml
Note that the compiler needs to access all compiled components that are imported, in order to perform its type checking (that also is the reason why the interactive toplevel had to load the signature of component Fac). We can run our little application using the Alice virtual machine:
alicerun Main Input number: 34 Evaluating component Fac... 295232799039604140847618609643520000000
You can again observe that imports are performed lazily. If the Fac component is never accessed, it will not be loaded at all:
alicerun Main Input number: gnalp error
A component carries its signature and the signatures of all its imports. You can inspect them using the Alice linker:
alicelink -d Main
import
structure TextIO :
sig
type instream
val inputLine : instream -> string option
val stdIn : instream
val print : string -> unit
end
from "x-alice:/lib/system/TextIO"
import
structure OS :
sig
structure Process :
sig
type status
val success : status
val failure : status
val exit : status -> 'a
end
end
from "x-alice:/lib/system/OS"
import structure Fac : sig val fac : int -> int end from "Fac"
structure Main : sig val main : unit -> OS.Process.status end
The output first lists all imports required by the component (which includes necessary parts of the library) and then the signature of its own export - in this case the last line. Note that import locations are actually denoted by URLs. In this tutorial we will only make use of file URLs, but components can actually be imported from arbitrary locations in the Internet via HTTP addresses.
Before a component is evaluated at runtime, its export signature is matched against the import signature of the component that imports and requests it. If that match fails, all references to items from the component are replaced by failed futures. We can observe this if we modify and recompile our Fac component in an incompatible way without adapting Main:
(* Fac.aml modified *)
structure Fac =
struct
val _ = print "Evaluating component Fac...\n"
fun fac (0,n) = n
| fac (i,n) = fac (i-1, i*n) (* tail-recursive *)
end
An attempt to run the application without adapting Main properly will cause a runtime failure:
alicec Fac.aml alicerun Main Input number: 20 Evaluating component Fac... error
An application that strives to be robust against such failures should handle the corresponding exceptions. See the manual pages on components for more details.
A way to avoid such errors is to statically link all components of the application using the static linker:
alicelink ./Main --include ./ -o LinkedMain.acl alicelink: signature of component ./Fac does not match import requirement of component ./Main Try recompiling the latter.
Oops! The linker verifies whether all import/export signatures are compatible. Of course, this is not the case since we intentionally made Fac incompatible. Recompiling Main, as the linker suggests, will not help either in this case.
But if we revert Fac to its original form and recompile it, the linker will happily accept it:
alicec Fac.aml alicelink ./Main --include ./ -o LinkedMain.acl
The linker builds a new component that bundles all components that are directly or indirectly imported by the root component given on the command line - in this case, Main - and that match the include pattern specified. See the manual page for details.
There is a close connection between components and pickles. Actually, they
are interchangable: a pickle
As a consequence, Alice enables the
structure Fac50 = struct val x = Fac.fac 50 end
structure Fac50 : sig val x : IntInf.int end
Pickle.save ("Fac50.alc",
pack (structure Fac50 = Fac50)
: (structure Fac50 : sig val x : IntInf.int end))
val it : unit = ()
Assume that calculating the factorial of 50 is an expensive computation. We have now performed it statically and generated a component that exports the result as a value. We may import it as usual:
import structure Fac50 from "Fac50" ### loaded signature from file:/home/rossberg/Fac50 structure Fac50 : sig val x : IntInf.int end = Fac50 Fac50.x val it : IntInf.int = _lazy await Fac50.x val it : IntInf.int = 30414093201713378043612608166064768844377641568960512000000000000
A pickle is an evaluated component. Evaluated components are closed, i.e. they never depend on any import:
alicelink -d Fac50 structure Fac50 : sig val x : int end
The linker shows that there is only an export signature to this component. See the manual pages on components for more information on evaluated components.
Linking of components is handled by the system's component manager. Applications may configure the component manager and the attached resolver to adapt to their needs, or may even set up their own component managers. Component managers essentially allow to achieve what is often called sandbox security for untrusted components. See the library reference for more detail.
The implementation of an interpreter for a simple functional language demonstrates how an application can be divided into components:
See readme.txt for build instructions.
Components and pickles already provide a primitive form of distributed programming, since they may be imported or loaded from arbitrary locations across a local network or even the Internet. But Alice also provides high-level means for processes at different sites to communicate directly.
The first mechanism that allows sites to establish peer-to-peer connections is offer and take. A process can create a package and make it available to other processes, for example the Num structure from the previous section:
val t = Remote.offer (pack Num : NUM) ### loaded signature from x-alice:/lib/distribution/Remote val t : ticket = "x-alice://134.96.186.172:46849/ticket/0"
Offering a package opens a communication port and returns an URI for that port. The URI is called a ticket. A ticket can be transferred to other sites, say by email or through some web document. Other sites can then obtain the available package using the ticket. Of course, the exporting site may also obtain it itself (which we will do in this interactive example for the sake of simplicity):
val p = Remote.take t
val p : Package.package = package{|...|}
structure Num' = unpack p : NUM
structure Num' : NUM
Num'.toInt (Num'.fromInt 444)
val it : int = 444
In general, take establishes a connection to the communication port denoted by the ticket, and retrieves the offered package. Transfer of the package is defined by the pickling/unpickling semantics, i.e. the whole closure of the package is transferred to the client, including any code representing embedded functions.
Tickets are intended merely as a means to establish an initial connection between sites. All subsequent communication should be dealt with by the functions in the offered package. Alice provides a very simple feature to enable this idiom: proxies. A proxy is basically an RPC stub, a mobile reference to a stationary function that can be used in place of the function it references.
The library function
Remote.proxy : ('a -> 'b) -> ('a -> 'b)
creates a proxy for an arbitrary function:
fun fib (0 | 1) = 1 | fib n = fib (n-1) + fib (n-2) val fib : int -> int = _fn val fib' = Remote.proxy fib val fib' : int -> int = _fn
The resulting function has the same type as the function it references. When it is applied, all arguments are forwarded to the original function, and the result is transferred back:
fib' 20 val it : int = 10946
Pickling a proxy does only pickle the respective reference and
As a most general example consider a compute server, a server which offers its computational resources to clients. Such a server can be described by the following signature:
signature COMPUTE_SERVER =
sig
val compute : ('a -> 'b) * 'a -> 'b
end
It can be given a function and an appropriate argument and it will compute the result of applying the function to the argument.
Such a server is easily set up by packaging the straight-forward implementation of this signature and offering it to other processes. A slight complication is that, due to ML's value restriction on polymorphic typing, we cannot use the proxy function to create a polymorphic proxy. Instead, we use the polymorphic functor
Remote.Proxy (signature S structure X : S) : S
that allows wrapping all functions in a structure into proxies in one go:
structure ComputeServer =
Remote.Proxy (signature S = COMPUTE_SERVER
structure X = (fun compute (f,x) = f x))
structure ComputeServer : COMPUTE_SERVER
val ticket = Remote.offer (pack ComputeServer : COMPUTE_SERVER)
val ticket : ticket = "x-alice://134.96.186.172:46849/ticket/1"
Assume that the local HTTP server's domain is www.mydomain.net and the root of its document tree is in directory /www of the local file system. The server may store the ticket as a WWW document:
Pickle.save ("/www/computeserver.ticket",
pack (val x = ticket) : (val x : string))
val it : unit = ()
A client can retrieve the (dynamically created) ticket from the (statically known) ticket URL:
structure Ticket = unpack Pickle.load "http://www.mydomain.net/computeserver.ticket"
: (val x : string)
structure Ticket : sig val x : string end
Note that we could perfectly well have exchanged the ticket in text form using ordinary file I/O, but pickling made it slightly more convenient.
The client can now establish a connection by taking the offered package and unpacking it under the agreed-upon signature:
structure Server = unpack Remote.take Ticket.x : COMPUTE_SERVER structure Server : COMPUTE_SERVER
Using the Server stub the client can shift its comutational load to the compute server:
Server.compute (fib, 30) val it : IntInf.int = 1346269
The application transfers the function fib, as well as the argument 30, to the server, which evaluates it. When it is done, it returns the result.
It is important to note that only establishing the initial connection requires a dynamic type check with this idiom! All subsequent uses of the transferred structure in general, and the contained proxy in particular do not require any check. Communication via proxies is always statically type-safe!
You will have noticed that the remote call to the server is synchronous, i.e. the client will not proceed before the server delivers the result. However, a synchronous call can trivially be transformed into an asynchronous one using functional threads!
spawn Server.compute (fib, 40) val it : int = _future
Functional threads and futures hence are a high-level mechanism to improve lag latency in distributed applications - a client can proceed concurrently to the server and has to suspend only when it actually requires the result of a remote operation that the server has not yet delivered.
Sometimes applications themselves need to create new processes at remote sites. This is known as remote execution. Remote execution can be initiated using the Run library functor. See the respective manual page for more about distribution in general and remote exection in particular.
Alice ML provides full support for state-of-the-art constraint programming technology. Constraint-based problem solving is a technique for solving hard combinatorial problems that can be stated as variables ranging over a finite domain of non-negative integers, or sets thereof. Problems in this class range from puzzles to real world applications as diverse as scheduling, ware house allocation, configuration and placement.
Let us take a look at programming with finite domain constraints. A finite domain (FD) is a set of natural (non-negative integer) numbers. An FD constraint is a formula in predicate logic, containing variables ranging over the natural numbers. In particular, a domain constraint is a constraint that restricts the domain of a particular variable. A finite domain problem is a finite set of quantifier-free constraints that contains a domain constraint for every variable occurring in it. A solution is a variable assignment that satisfies every constraint of the problem.
As a simple example of a complete program solving a finite domain problem, consider the Send More Money problem. It consists in finding distinct digits for the letters S, E, N, D, M, O, R, Y such that S and M are different from zero (no leading zeros) and the equation
SEND + MORE = MONEY
is satisfied. The unique solution of the problem is 9567 + 1085 = 10652.
Using Alice, the problem can be solved as follows. First, we have to import the constraint library and define a so-called script that encodes the problem:
import structure FD from "x-alice:/lib/gecode/FD"
import structure Linear from "x-alice:/lib/gecode/Linear"
open Linear
fun money sp =
let
val v as #[S,E,N,D,M,O,R,Y] = fdtermVec (sp, 8, [0`#9])
in
distinct (sp, v, FD.BND);
post (sp, S `<> `0, FD.BND);
post (sp, M `<> `0, FD.BND);
post (sp, `1000`*S `+ `100`*E `+ `10`*N `+ D `+
`1000`*M `+ `100`*O `+ `10`*R `+ E `=
`10000`*M `+ `1000`*O `+ `100`*N `+ `10`*E `+ Y, FD.BND);
branch (sp, v, FD.B_SIZE_MIN, FD.B_MIN);
{S,E,N,D,M,O,R,Y}
end
val money :
Linear.space ->
{D : term, E : term, M : term, N : term, O : term, R : term, S : term,
Y : term} = _fn
The Send More Money problem cannot be solved using constraint propagation alone. Search is required to reduce the problem space until constraint propagation is able to determine the solution. The distribute function in the script specifies the distribution strategy used when the problem space has to be split for search. See the Mozart Constraint Programming Tutorial for a more detailed explanation of the basic concepts.
To perform the actual search and obtain all solutions to the problem, predefined search engines can be used:
import structure Search from "x-alice:/lib/gecode/Search"
Search.searchAll money
val it :
Space.space list *
{D : term, E : term, M : term, N : term, O : term, R : term, S : term,
Y : term} =
([_val],
{D = FD (_val), E = FD (_val), M = FD (_val), N = FD (_val), O = FD (_val),
R = FD (_val), S = FD (_val), Y = FD (_val)})
The actual solutions could now be extracted from the result record using the functions from the FD.Reflect library structure. However, the easiest way to obtain the solutions is to interactively explore the search tree induced by the script using the Explorer instead of offline Search:
import structure Explorer from "x-alice:/lib/tools/Explorer" Explorer.exploreAll money val it : unit = ()
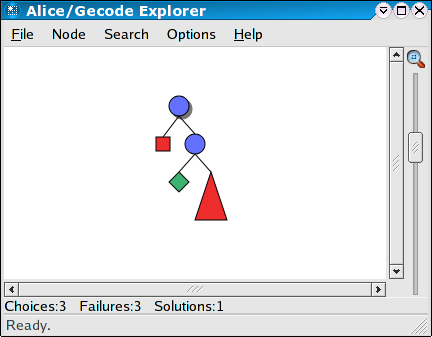
Double-clicking on the only solution node in the search tree (the green diamond) will open an Inspector window displaying the variable assignments of the solution.
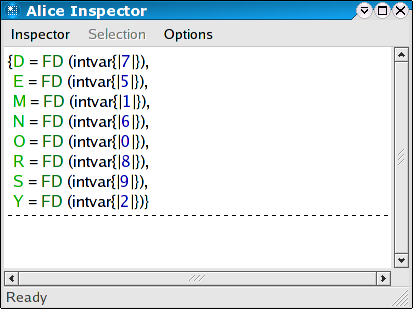
Chosing an inner node will display the information available at the respective point of the search tree.