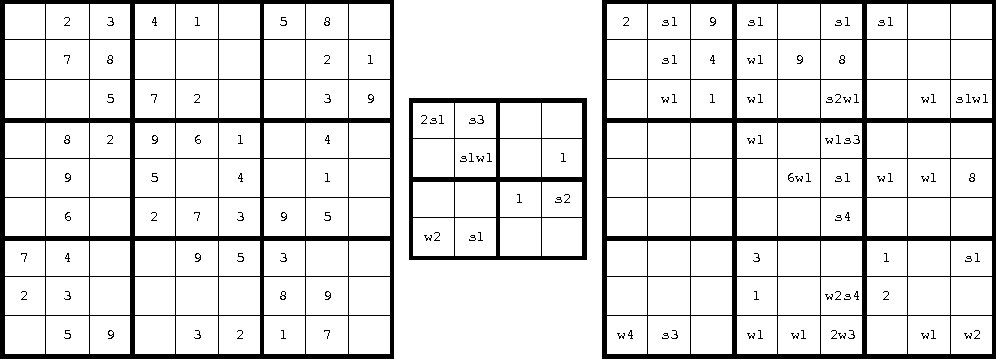
1. ábra
| BME Villamosmérnöki és Informatikai Kar
Mérnök-informatikus alapszak |
Nappali tagozat
2012/2013-es tanév, tavaszi félév
|
Sudoku-mátrixnak hívunk egy olyan négyzetes mátrixot, amelyben a sorok (és az oszlopok) száma egy n = k2 ≥ 1 négyzetszám. (Tehát a mátrix elemeinek száma n2 = k4.)
Egy Sudoku-mátrixban cellának hívunk egy olyan (folytonos) részmátrixot, amely k sorból és k oszlopból áll, és bal felső sarkának sor- ill. oszlopsorszáma i*k+1 ill. j*k+1, ahol 0 ≤ i,j ≤ k-1 (a sorokat és oszlopokat 1-től számozzuk). A cella mérete k.
A Sudoku-mátrix elemeit mezőknek is nevezzük.
Egy Sudoku-feladvány egy olyan Sudoku-mátrix, amelynek egyes mezői segítő információkat (röviden infókat) tartalmaznak. A Sudoku játék közismert alapváltozatában csak ún. száminfók fordulnak elő, amelyek azt írják elő, hogy a megoldás adott mezője egy adott számot tartalmazzon.
Egy n*n méretű Sudoku-feladvány teljes megoldása (vagy röviden: megoldása) egy olyan n*n-es Sudoku-mátrix, amelynek az alábbi feltételek egyszerre kielégíti:
A jelen házi feladatban a száminfók mellett további segítő információ fordulhat elő: a távolságinfó. Egy távolságinfó azt írja elő, hogy az adott mező értékének a megadott számértékkel kell különböznie az alatta, illetve a tőle balra levő mező értékétől. Egy mezőben egyfajta infóból legfeljebb egy lehet, tehát az egy mezőre vonatkozó infók száma 0-tól 3-ig terjedhet (ez a maximum úgy érhető el, hogy a mezőre egy száminfó és kétféle távolságinfó vonatkozik).
Példaként három Sudoku-feladványt mutatunk az 1. ábrán, ahol a k cellaméret rendre 3, 2, 3.

Az első feladványban csak száminfók vannak, mint a hagyományos Sudokuban. A második és harmadik feladványban vannak távolságinfók is, amelyeket egy betűvel és a betű után álló számmal jelölünk. Kétféle távolságinfó van, amelyek jelentése a következő:
si: az adott és az alatta levő mező értéke
közötti különbség abszolút értéke i (s = south),wi: az adott és a tőle balra levő mező értéke
közötti különbség abszolút értéke i (w = west). Ha egy mező tartalmaz i értékű távolságinfót, akkor azt mondjuk, hogy az adott mező és az infó által kijelölt szomszéd mező között i értékű távolságkorlát áll fenn. A távolságkorlát fogalma szimmetrikus, tehát ugyanilyen értékű korlátozás áll fenn a szomszéd és az infót tartalmazó mező között is.
A Sudoku-feladvány bal szélső oszlopának mezőiben is állhat wi, alsó
sorának mezőiben pedig si, annak ellenére, hogy nincs
hasznosítható jelentésük. Ezeket az infókat figyelmen
kívül kell hagyni.
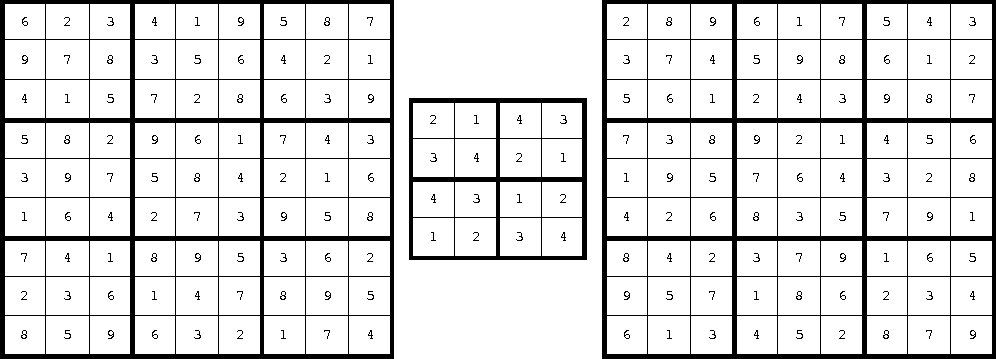
Az 1. ábrán látható három feladvány egy-egy megoldását a 2. ábra mutatja. Az első és a harmadik feladványnak van más megoldása is, a középsőnek az ábrán szereplő mátrix az egyetlen megoldása. Az infók nem-teljes voltára (lásd a fenti második megjegyzést) több példát is találhatunk ezekben a feladványokban.
Írjon sudoku néven olyan Prolog-eljárást, ill.
Erlang-függvényt, amely egy feladvány összes megoldását előállítja!
Feltételezheti, hogy a feladvány k cellamérete legfeljebb 10.
A Prolog-eljárásnak két paramétere van. Első (bemenő) paramétere a feladványt, második (kimenő) paramétere a megoldást írja le. Az eljárásnak a visszalépések során minden megoldást pontosan egyszer kell kiadnia (tetszőleges sorrendben). Ez azt is jelenti, hogy ha a feladványnak nincs megoldása, az eljárásnak meg kell hiúsulnia.
A Prolog-eljárás bemenő paramétere egy
s(K,T)
felépítésű struktúra, ahol
K a cellák oldalhossza,T a sorok listájaként megadott feladvány, ahol egy sor a benne
levő mezők listája.
A feladvány egy mezőjét infók listájaként adjuk meg. Infó lehet
az
s(I), a w(I) és a v(N)
struktúra, ahol I a távolságkorlát értéke,
és N az adott mező előírt értéke (a
v rövidítés az angol value szóból származik). Az
infók listájában mindegyik struktúra legfeljebb egyszer,
de tetszőleges sorrendben fordulhat elő, és a lista üres is lehet.
A Prolog-eljárás kimenő paramétere a feladvány egy megoldása, amelyet számokat tartalmazó listák listájaként ábrázolunk.
Például az 1. ábra középső feladványát a következő Prolog-struktúrával írjuk le:
s(2, [[[v(2),s(1)], [s(3)], [], []],
[ [], [s(1),w(1)], [], [v(1)]],
[ [], [], [v(1)], [s(2)]],
[ [w(2)], [s(1)], [], []]])
A feladvány egyetlen megoldását a következő lista írja le:
[[ 2, 1, 4, 3],
[ 3, 4, 2, 1],
[ 4, 3, 1, 2],
[ 1, 2, 3, 4]]
Az Erlang-függvény egyetlen paramétere a feladványt, az eredménye a megoldásokat írja le. Az eredménylistának a feladvány összes megoldását tartalmaznia kell, mégpedig minden megoldást pontosan egyszer (tetszőleges sorrendben). Ez azt is jelenti, hogy ha a feladványnak nincs megoldása, az eredmény az üres lista kell legyen.
Az Erlang-függvény paramétere egy {K,T} pár, ahol K
és T jelentése azonos a Prolog-eljárás K és
T struktúraelemeinek a jelentésével.
A feladványban minden mező infók listáját tartalmazza. Infó
{s,I}, {w,I} vagy {v,N}
alakú pár, ahol I, illetve
N jelentése azonos a Prolog-eljárás I, illetve
N struktúraelemének a jelentésével. Az
infók listájában az elemek sorrendje itt is tetszőleges.
Az Erlang-függvény eredménye a feladvány összes megoldásának listája, ahol mindegyik megoldást számokat tartalmazó listák listájaként ábrázolunk.
Például az 1. ábra középső feladványát a következő Erlang-párral írjuk le:
{2, [[[{v,2},{s,1}], [{s,3}], [], []],
[ [], [{s,1},{w,1}], [], [{v,1}]],
[ [], [], [{v,1}], [{s,2}]],
[ [{w,2}], [{s,1}], [], []]]}
A feladvány egyetlen megoldását tartalmazó lista a következő:
[[[ 2, 1, 4, 3],
[ 3, 4, 2, 1],
[ 4, 3, 1, 2],
[ 1, 2, 3, 4]]]
A házi feladat megoldása során a feladványt megadó bemenő paraméterre vonatkozó formai előírások meglétét nem kell ellenőriznie, azaz feltételezheti, hogy a paraméter megfelel a fent ismertetett formai követelményeknek.
A sudoku/2 Prolog-eljárás típusát a következő -
megjegyzésként megadott - Prolog-típusdefiníciók írják le.
% :- type sspec ---> s(size, board).
% :- type size == int.
% :- type field == list(info).
% :- type info ---> s(int); w(int); v(int).
% :- type board == list(list(field)).
% :- type ssol == list(list(int)).
% sudoku(SSpec, SSol):
% SSol az SSpec feladványt kielégítő megoldás.
% :- pred sudoku(sspec::in, ssol::out).
A sudoku:sudoku/1 Erlang-függvény típusát a következő -
megjegyzésként megadott - Erlang-típusdefiníciók írják le.
%% @type sspec() = {size(), board()}.
%% @type size() = integer().
%% @type field() = [info()].
%% @type info() = {s, integer()} | {w, integer()} | {v, integer()}.
%% @type board() = [[field()]].
%% @type ssol() = [[integer()]].
%% @spec sudoku:sudoku(SSpec::sspec()) -> SSols::[ssol()].
%% @doc SSols az SSpec feladványt kielégítő megoldások listája.
A programot tartalmazó modul két attribútuma ez legyen:
-module(sudoku). -export([sudoku/1]).
Programjait keretprogramok segítségével próbálhatja ki. A keretprogramokat a beadáskor használthoz hasonló tesztesetekkel együtt töltheti le:
A keretprogram bemenete egy olyan szövegfájl, amelynek első nem üres sora a
Sudoku-feladvány cellaméretét, minden egyes további nem üres sora a
Sudoku-feladvány egy-egy sorát tartalmazza, ahol az egyes mezők értékét egy
vagy több szóköz választja el. A - karakter jelzi, ha egy
mező nem tartalmaz infót. Ha tartalmaz, a mezőt az infók felsorolásával
írjuk le: először a száminfót adjuk meg decimális számként, majd
a távolságinfókat. Az utóbbiak ábrázolása a következő: először az
s vagy w betűjelet írjuk
le, ezt követően pedig a távolságot decimális számként. A távolságérték
elhagyható, alapértelmezése 1. Az egy mezőhöz tartozó infók leírásában
szóköz nem szerepelhet.
Például az 1. ábra közepső Sudoku-feladványát a 3. ábrán látható módon ábrázoljuk a bemeneti szövegfájlban:
2 2s s3 - - - s1w - 1 - - 1 s2 w2 s - -3. ábra
A keretprogram kimenete a 4. ábrán bemutatotthoz hasonló tartalmú szövegfájl.
----- 2 1 4 3 3 4 2 1 4 3 1 2 1 2 3 4 -----4. ábra
A ksudoku.pl Prolog-keretprogram a következő eljárásokat
exportálja:
% :- pred sudoku_be(file::in, sspec::out).% :- pred sudoku_ki(file::in, ssol::in).% :- pred megold(file::in, file::in).sudoku/2 eljárást.% :- pred stopper(file::in, file::in).megold/2, de a végén kiírja a feladvány nevét, a
megoldások számát és a futási időt is.
% :- pred teljes_teszt(int::in).
tests könyvtárban levő összes testXXXd.txt
tesztállomány esetén:
testXXXs.txt állományban megadott
megoldáshalmazt kapta,
megold/2) kiírja az eredményt a tests_out
könyvtár testXXXt.txt nevű állományába.
XXX egy tetszőleges hosszúságú
számjegysorozatot jelöl.
A keretprogram felhasználja a file típust:
% :- type file == atom.
A file típusú paraméterben a user atomot megadva
a terminálról vihetünk be, ill. a terminálra írathatunk ki adatokat.
Egyébként a megadott nevű fájlba írunk, ill. fájlból olvasunk.
Használat: saját programját a
sudoku.pl nevű fájlba tegye, különben a
ksudoku.pl keretprogram nem találja meg. Ezután futtassa a
SICStus interpretert, és töltse be a keretprogramot. Példa:
SICStus 4.2.1 (x86-linux-glibc2.5): Wed Feb 1 01:12:14 CET 2012
Licensed to BUTE DP Course
| ?- [ksudoku].
% consulting d:/dokumentumok/bme/dp/ksudoku.pl...
% module sudoku_frame imported into user
% loading e:/programozas/sicstus/library/lists.po...
% module lists imported into sudoku_frame
% loaded e:/programozas/sicstus/library/lists.po in module lists, 15 msec 11688 bytes
% consulted d:/dokumentumok/bme/dp/ksudoku.pl in module sudoku_keret, 15 msec 29792 bytes
yes
| ?- stopper('teszt0.txt','teszt0.sol').
A stopper/2, ill. megold/2 eljárások meghívása a
sudoku.pl programot automatikusan betölti (ha szükséges),
ezért ennek módosításakor nem kell sem a SICStus interpretert
újraindítania, sem a keretprogramot újra betöltenie.
A ksudoku.erl Erlang-keretprogram a következő függvényeket
exportálja:
@spec ksudoku:sudoku_be(FileIn::string()) -> SSpec::sspec()SSpec a FileIn szövegfájlból beolvasott
Sudoku-feladvány.@spec ksudoku:sudoku_ki(FileOut::string(), SSols::[ssol()]) -> void()SSols listában átadott Sudoku-megoldásokat kiírja a
FileOut szövegfájlba.@spec ksudoku:megold(FileIn::string(), FileOut::string()) -> void()FileIn szövegfájlból és összes
megoldását kiírja a FileOut szövegfájlba. Ehhez felhasználja
a sudoku:sudoku/1 függvényt.@spec ksudoku:stopper(FileIn::string(), FileOut::string()) -> void()ksudoku:megold/2, de a végén kiírja a
FileIn nevét, a megoldások számát és a futási időt is.
@spec teljes_teszt(Timeout::integer()) ->
[done|timeout].
tests könyvtárban levő összes testXXXd.txt
tesztállomány esetén:
Timeout másodperces időkorláttal,
testXXXs.txt állományban megadott
megoldáshalmazt kapta,
megold/2) kiírja az eredményt a tests_out
könyvtár testXXXt.txt nevű állományába.
XXX egy tetszőleges hosszúságú
számjegysorozatot jelöl.
Használat: saját sudoku.erl nevű programját
minden változtatás után fordítsa le,
és sudoku.beam néven rakja a keretprogrammal
azonos mappába, különben a ksudoku.erl keretprogram nem
találja meg. Ezután indítsa el az Erlang interpretert, és töltse be a
lefordított keretprogramot. Példa:
Eshell V5.8 (abort with ^G)
1> l(ksudoku).
{module,ksudoku}
2> ksudoku:stopper("teszt0.txt","teszt0.sol").
A keretprogram automatikusan betölti a sudoku.beam programot,
feltéve, hogy a keretprogrammal azonos mappában van.
Ha a saját sudoku.erl programját módosítja, a lefordítása után
betöltheti az l(sudoku). paranccsal, de újra betöltheti a
ksudoku.erl keretprogramot is, ami magával húzza a módosított
programot. Egyes esetekben célszerű újraindítani az Erlang értelmezőt.
Mindkét programot úgy írja meg (választása szerint vagy magyarul, vagy angolul), hogy a szövegük jól olvasható legyen: válasszon értelmes neveket, specifikálja a paraméterek és más azonosítók szerepét és értelmezési tartományát, magyarázza meg az egyes eljárások, ill. függvények feladatát és működését! Kövesse a Prolog-, ill. az Erlang-diákon használt szövegelrendezési konvenciókat! Javasoljuk, hogy ne írjon 72 karakternél hosszabb sorokat. Minden eljáráshoz és függvényhez készítsen fejkommentet!
A két programhoz készítsen közös dokumentációt; vagy magyarul, vagy angolul. A dokumentáció tartalma legalább a következő legyen:
Fogalmazzon világosan és tömören, ügyeljen a helyes nyelvhasználatra és a helyesírási szabályok betartására! Az indokoltan elvárható formai követelmények be nem tartását, a gondatlan kivitelt szankcionáljuk.
A dokumentációt elektronikus alakban adja be HTML, PDF, esetleg ASCII formátumban.
A programok készülhetnek MS Windows alatt is, de Linux alatt is működniük kell. A beadott programokat Linux környezetben a SICStus Prolog 4.2.x, ill. az Erlang/OTP R14A rendszerekkel teszteljük.
Megoldásában Prolog nyelven tetszőleges könyvtárakat használhat, kivéve a
clpfd, clpq, clpr, clpb
és chr Prolog-könyvtárakat: az ezeket a
könyvtárakat felhasználó megoldások a létraversenyben nem vehetnek részt,
és így megajánlott jegyet sem kaphatnak.
Erlang nyelven az adatbázist vagy egyéb mellékhatást használó függvények használata tilos (erlang:get, erlang:put, digraph modul, io modul stb.). Néhány megengedett, állapotmentes modul: array, dict, gb_*, lists, math, ord*, queue, sets, string.
A programokat és az elektronikus dokumentációt webes felületen lehet külön-külön feltölteni az Elektronikus Tanársegéd HF beadás menüpontjában. A beadást többször is megismételheti, az utoljára beadott megoldást tekintjük érvényesnek.
Programját egy tízelemű tesztsorozattal automatikusan futtatjuk. A teszteseteket úgy választjuk meg, hogy legalább négy feladványt a kevésbé ötletes programok is meg tudjanak oldani. Az eredményt levélben közöljük és az ETS-ben is megnézhető.
A nagy házi feladat elkészítése nem kötelező, de megoldását mindenkinek javasoljuk: ez a deklaratív nyelvek magas szintű elsajátítását nagy mértékben segíti.
A beadási határidők:A beadási határidő után értékeljük a programokat (ez az ún. "éles" teszt). Ehhez a beadási tesztsorozathoz hasonló nehézségű teszteseteket használunk. Az időkorláton belül helyes eredményt adó tesztesetek mindegyikére 0,5–0,5 pontot adunk, a 10 tesztesetre tehát nyelvenként összesen maximum 5 pontot. Ezen felül a dokumentációt, a programkód olvashatóságát, kommentezettségét is értékeljük, nyelvenként maximum 2,5 ponttal. A mindkét nyelven beadott nagy házi feladatra tehát maximum 15 pont kapható (ez 15%-a a pluszpontok nélkül elérhető legfeljebb 100 alappontnak).
Azok a programok, amelyek az éles teszt legalább 8 feladatát helyesen és az előírt időkorláton belül megoldják, létraversenyben vesznek részt. A leggyorsabban futó Erlang-, ill. Prolog-programokra - helyezési számuktól függően - külön-külön 7,5 és 0,5 közötti pluszpont kapható. Ha valaki tehát mindkét nyelvből a leggyorsabb programot írja meg, akkor a 100 alapponton felül 15 pluszpontot kap.
Azok a hallgatók, akik mindkét nyelvből bejutnak a létraversenybe - a tantárgyi adatlapon leírt feltételek fennállása esetén - megajánlott jegyet kapnak.
A programot és dokumentációt mindenkinek saját magának kell elkészítenie. A beadott nagy házi feladatokat gépi úton hasonlítjuk össze, másolás esetén fegyelmi eljárást kezdeményezünk. Az algoritmusra vonatkozó ötletek cseréjét viszont nem tiltjuk.